Blog
Aperiyodik Monotil: Geometrinin Kutsal Kasesi Einstein veya Şapka şekli
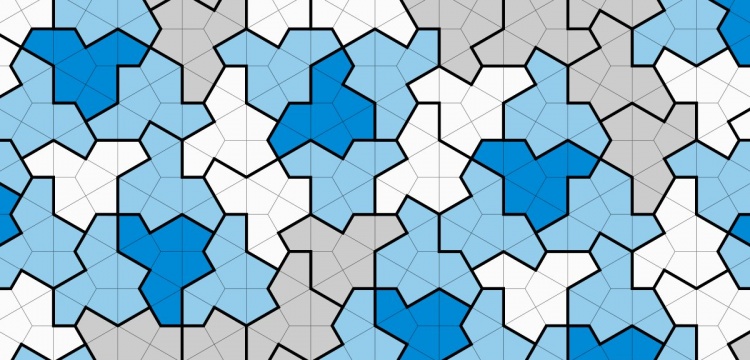
Aperiyodik monotil, yaklaşık 60 yıldır çözülemeyen bir problemi sonuçlandırmıştır: “Tek bir şekil, tekrarsız olarak düzlemi kaplayabilir mi?”
www.arkeolojikhaber.com
Aperiyodik Monotil, matematiksel ve teknik bir terimdir. Einstein ise bu kavram için kullanılan, popüler ve espri amaçlı takma isim. Bu isim, Almanca'da "ein Stein" (tek taş / karo) anlamına gelir ve ünlü bilim insanı Albert Einstein ile bir ilgisi yoktur. Ancak kelime oyunu nedeniyle sıkça karıştırılır. Her iki kavram da düzlemi sadece tekrarlamayan bir şekilde döşeyebilen tek bir şekli ifade eder ve Millat'tan Sonra 2 Binlere kadar böyle bir şeklin imkansız olduğu sanılıyordu.
Aperiyodik Monotil; Tek bir şekil (monotil) kullanarak düzlemi, hiçbir tekrarlayan (periyodik) desen oluşturmadan tamamen kaplayan geometrik şekildir.
Aperiyodik Monotil; kelime anlamı olarak "Periodik Olmayan Tek Şekil" anlamında gelse de deyim olarak "Asla Tekrarlanmayan Şekil" , geometri ve döşeme (tessellation) matematiği ile ilgili çok özel ve önemli bir sorunun çözümünü sağlayan kavramdır ve popüler kültürde "Einstein Karosu" olarak adlandırılır.
Uygulama Alanları: Matematiksel geometri ve topoloji. Kristalografi (özellikle quasicrystal yapılar). Malzeme bilimi – atomik düzeyde tekrarsız dizilimlerin (örneğin kuazikristallerin) modellenmesi. Bilgisayar grafikleri ve tasarım. Estetik tasarım – özellikle mimari yüzeylerde tekrarsız mozaikl
Matematiksel Önemi
Aperiyodik monotil, yaklaşık 60 yıldır çözülemeyen bir problemi sonuçlandırmıştır: “Tek bir şekil, tekrarsız olarak düzlemi kaplayabilir mi?”
Bu soru ilk kez 1960’larda Roger Penrose tarafından ortaya atılan aperiyodik karo setleri (örneğin “Penrose Tiles” – iki farklı şekil kullanılarak yapılan tekrarsız döşemeler) üzerinden gündeme gelmişti. Ancak o dönemde hep birden fazla karo gerekiyordu.
Monotil (einstein) Nedir?
Monotil kelimesi, Latince ve Yunanca kökenli olup, Almanca'da "ein Stein" (tek taş/tek parça) anlamına gelen bir kelime oyunudur ve matematikteki anlamı şudur: Tek Bir Şekil (Fayans/Karo): Bir düzlemi (sonsuz bir yüzeyi) yalnızca o tek şekli kullanarak boşluksuz ve üst üste binmesiz bir şekilde döşeyebilen bir prototip karodur.
Aperiyodik Monotil (Einstein Karosu) Nedir? ,
Bu, monotil kavramının en zorlu alt kümesidir:
Aperiyodik: Asla tekrarlamayan bir desen oluşturan demektir. Yani, döşenen deseni ne kadar ötelerseniz öteleyin, kendini tam olarak kopyalayan bir nokta veya blok bulunamaz.
Aperiyodik Monotil ("Einstein"): Bir düzlemi boşluksuz kaplayabilen, ancak bu döşemenin ASLA periyodik (yani tekrarlayan) bir desen oluşturmasına izin vermeyen tek bir şekildir. (“Bir taş” anlamında Almanca ein Stein kelime oyunudur; fizikçi Einstein’la ilgisi yoktur.)
Uzun Süredir Çözümü Aranan Problem:
Matematikçiler (özellikle Penrose döşemelerinin keşfinden sonra) uzun yıllar boyunca, yalnızca tek bir tür karodan oluşan, periyodikliği zorla engelleyen bir şeklin var olup olmadığını merak etmişlerdir. Bu şekle, Almanca bir kelime oyunu olarak "einstein" (tek taş) adı verilmiştir.
"Şapka" ve "Metatiller" Nedir?
Bu zorlu problem 2023'te David Smith, Joseph Samuel Myers, Craig S. Kaplan ve Chaim Goodman-Strauss tarafından çözüldü: "Şapka" (The Hat): Keşfedilen ve aperiyodik monotil olduğu kanıtlanan, 13 kenarlı bir polikit (bir tür düzgün çokgen). Bu şekil, düzlemi tek başına döşeyebilir, ancak bunu yalnızca aperiyodik (tekrarlamayan) bir hiyerarşik yapı içinde yapabilir.
"Metatiller" (Metatiles): "Şapka" karolarının bir araya gelerek oluşturduğu, daha büyük kümeler veya yamalardır. Makale, bu metatillerin kendilerinin de daha büyük yapılar oluşturabildiğini (bir ikame kuralı ile) göstererek, tüm döşemenin sonsuz bir hiyerarşi içinde aperiyodik olduğunu kanıtlar.
"Şapka" ise, bu tanıma uyan ve 2023'te keşfedilen ilk gerçek örnektir.
2023’te David Smith adlı bir amatör matematikçi, İngiltere’de kendi tasarladığı bir şeklin (13 kenarlı bir tür eşkenar olmayan poligonun) düzlemi aperiyodik biçimde döşeyebildiğini fark etti.
Bu şekil daha sonra Craig S. Kaplan, Joseph Samuel Myers ve Chaim Goodman-Strauss gibi matematikçilerle birlikte incelendi.
Özellikleri
Şekil, 13 kenarlı bir poligondur (resmî olarak aperiodic monotile number 1 veya einstein tile).
Yalnızca tek tip karo kullanılarak düzlemi kaplar.
Hiçbir şekilde tekrarlayan düzen oluşturmaz.
Döşemeler yansıtılarak (ayna görüntüsüyle) da kullanılabilir.
“Kürek” biçimine benzediği için halk arasında “the hat” (şapka) olarak da anılır.
2024 yılında aynı araştırma ekibi, “the turtle” (kaplumbağa) gibi varyantlarını da bulmuştur.


Bu yazı hakkında yorum bulunamamıştır. İlk yorumu siz ekleyebilirsiniz >